金桔
金币
威望
贡献
回帖0
精华
在线时间 小时
|
本人岗位是Sourcing,岗位对专业性有要求,要求需要了解各生产物料的相关专业知识。关于四极杆有看过一些文献,我不是专业做研发的,但也想尝试回答下这个问题。以下是以前我的个人看完文献后的一些理解,如果有不对的地方,希望有大神可以指正。
先谈下我理解的原理,后面谈公式推导:
- 先简单的说,带电粒子在电场中会受到力的作用,当带电粒子至于相关的电场下,就会受到相应的力的作用,致使其发生相关的运动。 举一个不恰当的、但方便理解的例子:把此时的带电粒子比作你自己,电场比作左右两面人墙,当你想从左右两面人墙之间穿过去时,你刚以一定的初速度跑进去,结果发现左边站的都是美女,她们一直在叫你、拉你,右边站的都是抠脚大汉,他们一直嫌弃、推开你。作为一个男性你被吸引,自然而然的开始向美女这边走动,被拉扯。你可能会被左边的美女扣下,也有可能谁也留不住你你直接穿墙而过,这跟你的初速度和体重有关。
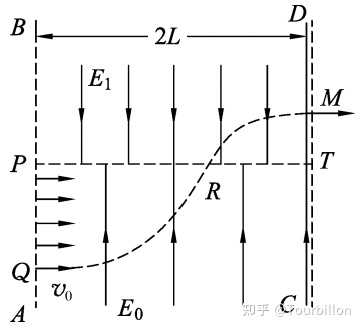
初始速度与电场方向不共线时,运动轨迹为抛物线,抛物线的开口方向朝向带电粒子的受力方向
2. 我们将电场再复杂化,创造出一个射频四极电场(该电场强度可调控,可以使一定质荷比的带电粒子发生相应的运动,从而对离子进行筛选和聚焦) 继续举一个不恰当的、但方便理解的例子:你还是那个带电粒子,你这时要以一定的初速度穿过上、下、左、右四面人墙,上下坐着的是大汉,左右坐着的是美女,但美女和大汉的位置可以以一定的频率对换,也就是上一秒上下是大汉、左右是美女,下一秒就可能上下是美女,左右是大汉。美女一直在呼唤你、拉你,大汉一直在嫌弃你、推你,而他们的位置又一直在变换,就导致你也一直在向前跑的同时,上下左右地被推过去拉过来。跟你一样的带电粒子还有其他人,你们身高、体重、长相、性格各不一样,有些人注定要在这种花里胡哨的环境中中途被留下、被抛弃到不了前方,而有些天选之人则在极致拉扯之中顺利通过人墙、到达前方。被留下和顺利通过的人都不要觉得一切都不可预知,实际上你们一开始就被设定好结局的。上帝让你留下你就自然而然的留下,上帝让你通过,你就自然而然的通过。
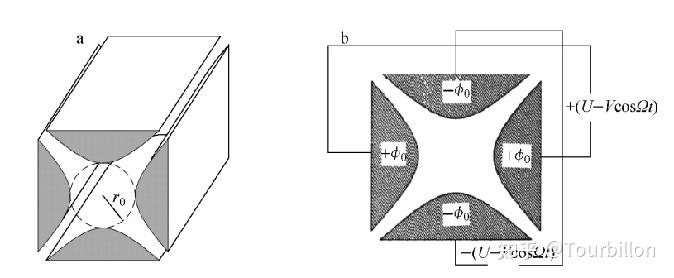
四极杆电极系统的理论是由pual等于1958年创立 的,提出了利用射频四极电场过滤离子的原理,根据他们的假设和理论研究,证明了可以在一定空间内产生“纯净”理想四极电场分布的四极杆电极系统,但必须是由4根几何形状完全等同,且包含双曲面截面的电极平行围绕着一个中心对称轴合围而成
接下来谈谈公式推导,有些公式我能推导出来,有些确实不懂,只要大家能懂整个推导的逻辑就行:
- 先设四极场中电场强度 :E=E0(λx+σy+γz)
λ、σ、γ是空间各坐标的权重常数,E0是与时间有关而与空间坐标无关的电场强度分量(就是上帝一直在控制男女对换位置,并且男女的推力和拉力大小也是可以调整的,只跟频率有关)
2. 根据 Laplace方程ᐁ2Φ=0 以及 E=—ᐁΦ( Laplace方程是液面曲率和水面压强的关系方程,这里为啥要用这个方程来求解呢,从逻辑上讲,我理解到的是电场也是个立体的场,随着离场中心距离的不同它在不同的位置也有相应的曲面的场强,而电场的这么个存在可以用拉普拉斯方程来模拟,然后根据拉普拉斯方程求得不同坐标的电场强度)
可得到解

解i针对离子阱,解ii针对四极杆
3. 根据电场强度,可以推导出电势分布函数Φ=1/2E0(λx2+σy2+γz2)+c,把解ii代入电势分布函数得到(我不知道怎么推导的,但逻辑就是通过比拟拉普拉斯方程求得电场强度,然后根据电场强度求的电势分布)
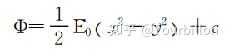
电势分布公式
进而得到公式( 我觉得可能跟这个公式E=—ᐁΦ有关,但我不知道怎么推导,看文献也没找到个过程,总之我理解的逻辑上是为了消除电场强度E0这个变量)
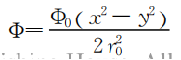
电势分布公式
然后取特殊值(我理解是为了将角频率ω引入,因为角频率是人为控制的。ω变化—某点的电势也在变化——离子的运动轨迹也跟着变化,后面就要把离子的运动轨迹给求出来了)
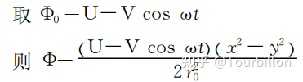
然后得到Mathieu方程:
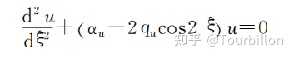
根据Mathieu方程求的解
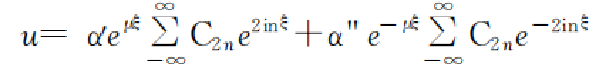
其中其中,α',α"为积分常数,取决于初始条件; 常数 C2n与μ取决于a和q的值,与初始条件无关,u即为 x或 y
而:
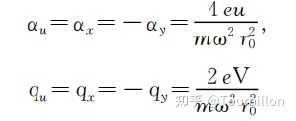
m为离子的质量;e为离子所带的电荷量;U、V 分别为电极上所接入射频信号Ф0的直流分量和交流分量;r0为四极场中心到极杆的最小距离,称为四极场半径,ω为射频电源的角频率
对于u来说1. 如果 μ有限,当 ξ→∞时方程有稳定解,此时,若离子最大位移 umax<r0,即离子未到达分析器边界, 则该离子可稳定通过四极杆区域,到达离子系统;2. 如果μ无限,当 ξ→∞时方程无稳定解,离子将被极杆吸收或逃逸而无法到达离子检测系统;3. 当μ=iβ且β为非整数时,离子具有稳定的周期性运动轨迹;4. 当β为整数时,离子轨迹虽具有周期性但不稳定,这对应于稳定性图中稳定区域与非稳定区域的分界线,如下图:
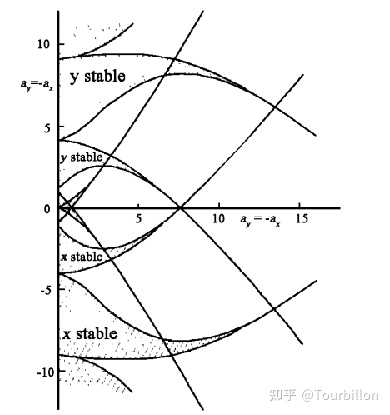
再进一步谈到质谱里常用的第一稳定区域:
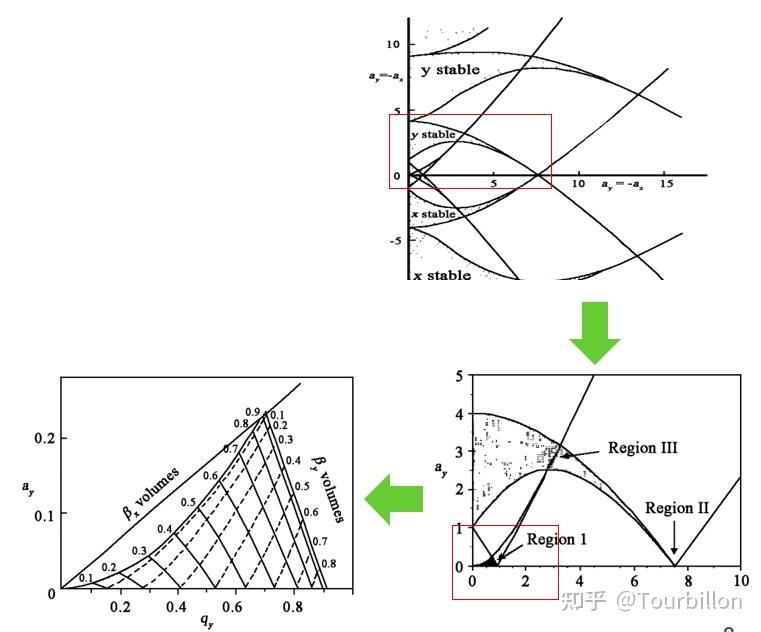
一步一步放大给你们看那个第一稳定区域
在四极杆质量分析器中,最常用的是原点附近的第I稳定区。在第Ⅰ稳定区内所有(a,q)点 对应的μ值都为纯虚数iβ的形式,且0<β<1。β单值取决于a和q,把稳定区内具有相同β值的 (a,q)点连成线,即得到等β线。可见,第I稳定区的边界分别为β=0和β=1的等β线。 第Ⅰ稳定区的形状大致像一个三角形,称 其为稳定性三角形。只要 a,q的绝对值都处于该三角形中,则离子具有稳定的轨迹,此时,符合初始入射条件的离子将稳定通过四极场,到达离子检测系统。
还有关于扫描线、质量范围、分辨率什么的,就暂时不多说了。公式推导这块,我只在理解逻辑和过程,至于具体怎么计算的,我不是专业的,确实不会。上面回答如果有哪里不对的地方,请大家指正。 |
|
 /3
/3 