如何用易懂的语言解释区间估计和假设检验的区别和联系？

心中u你

另外还有置信水平和显著水平的联系。
1-置信水平==显著水平？
===============================
今天翻浙大的概率论，看到有一个小节专门讲这个。。。

原文地址：https://www.zhihu.com/question/26415058

同花顺

统计推断有两大法宝:一是参数估计，二是假设检验。



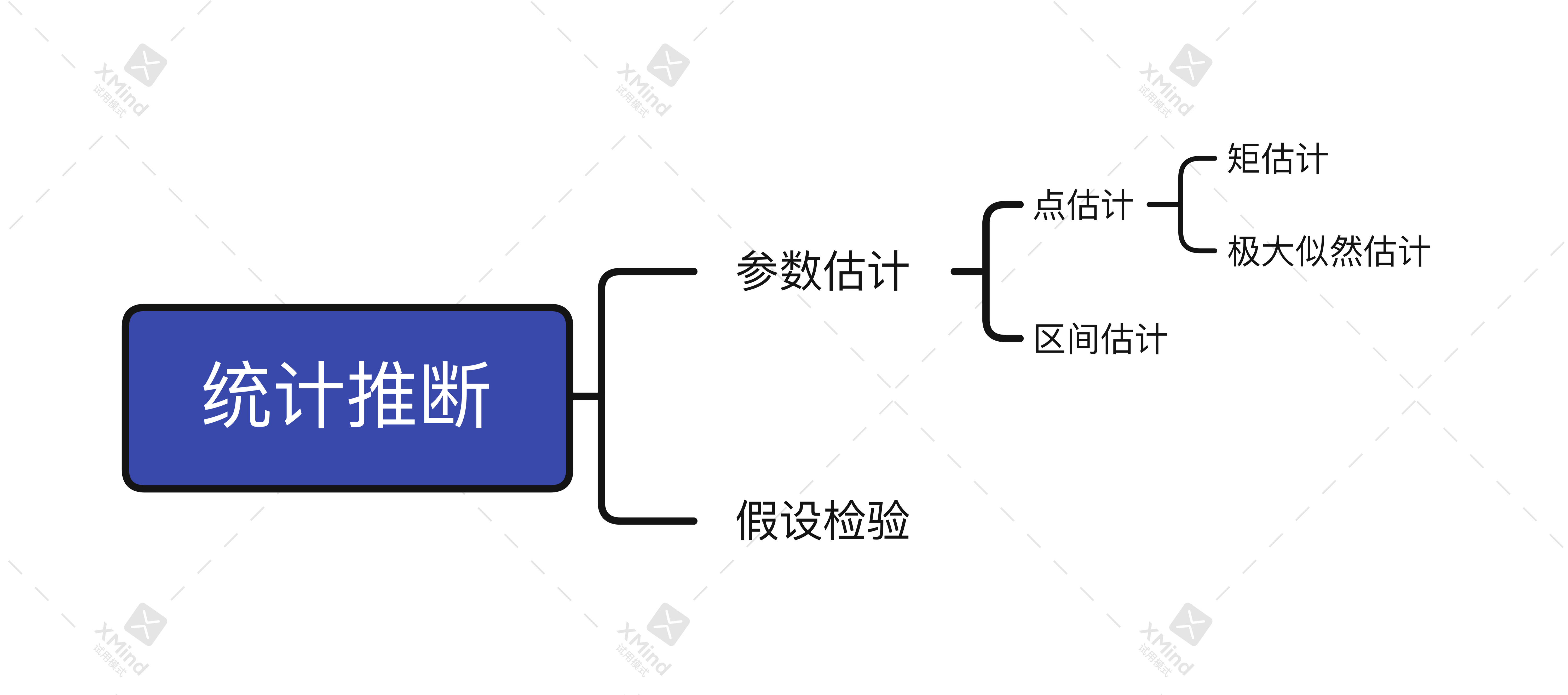
参数估计的本质是用样本统计量来估计总体的参数。统计量是样本场景名词， 具有样本的含义， 同样参数是总体场景名词， 具有总体的含义。比如： 样本的方差是一个统计量，总体 的方差是一个参数。

假设检验是根据样本统计量来检验对总体参数的先验假设是否成立。先验假设有很明确的主观目的，去对假设做证伪，常见的量化指标是P值。

参数估计中包含：
点估计：用样本统计统计量直接作为总体参数的估计值，简洁却存在以偏概全的局限性，包含我们常见的矩估计，极大似然估计。
区间估计：在预先给定的置信度（1-置信水平），比如90%､ 95%､ 99%.计算出总体参数的置信区间。
在总体标准差未知，我们常常可以选择t分布。当总体标准差已知或样本量(n大于50）很大时，我们可以选择正态分布。

假设检验：
1，提出检验假设（原假设及备择假设）。
2，确定检验的置信水平。
3，确定统计量与验证方法（Z检验，T检验，卡方检验等）。
4，计算出P值。
3，推断结论：基于P值与置信水平的大小判断结果。

案例实战：


这里使用R工具：
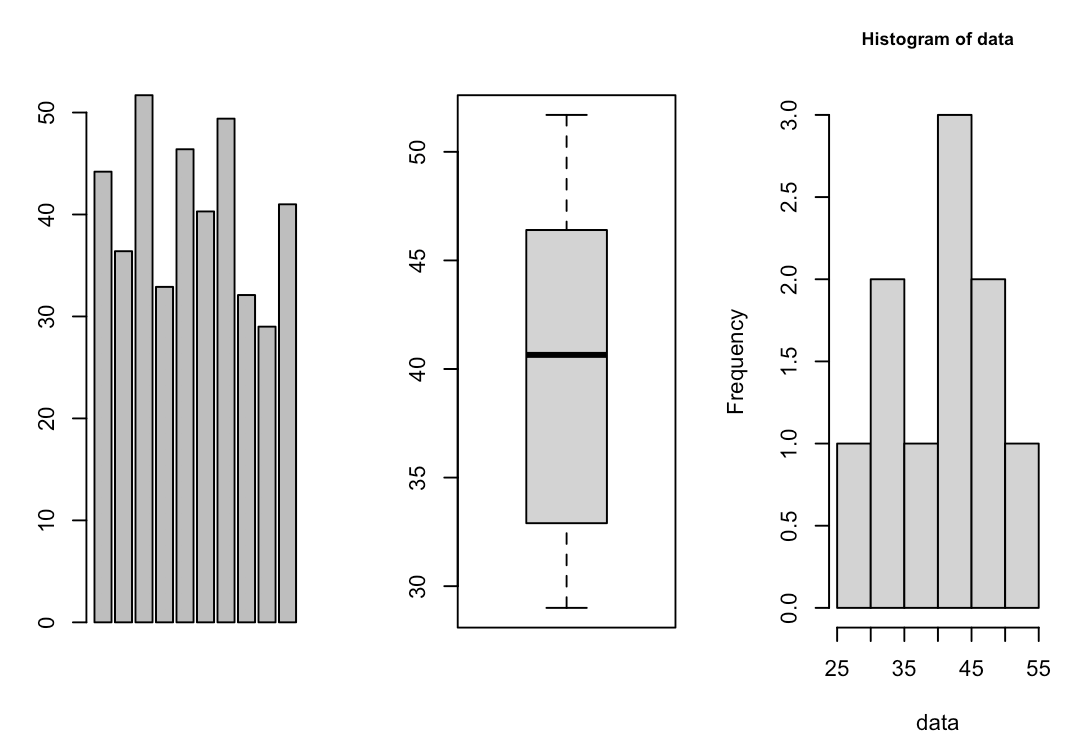
数值变量，我们可以绘制条形图，箱线图及分组后的直方图：
data<-c(44.2,36.4,51.7,32.9,46.4,40.3,49.4,32.1,29.0,41.0)
> par(mfrow=c(1,3), mai=c(0.7,0.7,0.6,0.1),cex=0.7,cex.main=0.8)
> barplot(data)
> boxplot(data)
> hist(data)

> data<-c(44.2,36.4,51.7,32.9,46.4,40.3,49.4,32.1,29.0,41.0,46.2)
> summary(data)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
  29.00   34.65   41.00   40.87   46.30   51.70

从summary数据总览可以看出：中位数 41.00 ，平均数 40.87，没有数值相同的众数。
参数估计：样本量为10，属于小样本量，总体标准差未知，这里可以使用t分布来估计总体均值。在给定的置信水平a=0.05，t=2.262。


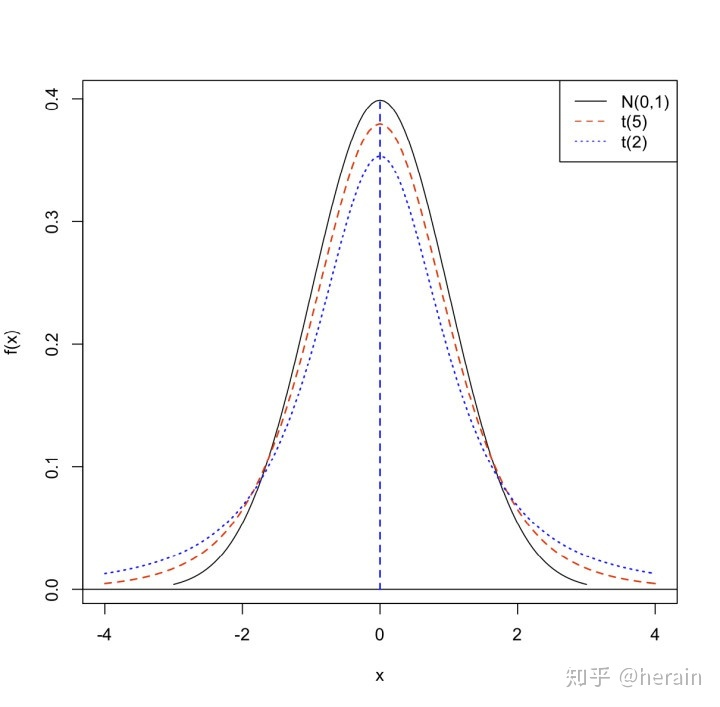
用公式计算 置信区间：

在置信水平为0.05条件下，破案率的置信区间为：[32.66,48.02]。由于破案率：46.2在置信区间中，所以与其他州的破案率没有明显区别。

假设检验：
1，提出检验假设（原假设及备择假设）：
H0 克雷默市破案率 与 其他10个城市平均破案率 无明显区别；H1 克雷默市破案率 与 其他10个城市平均破案率 有明显区别。
2，确定检验的置信水平：a=0.05，参考t值=2.262
3，确定统计量与验证方法：统计量为：t

4，计算出P值：P<0.05 (由计算的t值大于参考t值，可以的P值小于0.05)
3，推断结论：有P<0.05，这里拒绝原假设，选择备择假设 （如果样本纳入克雷默市破案率会得出相反的结论）。

这里我们推荐使用R来计算置信区间及P值：
library(BSDA)
#正态分布的置信区间求法
interval_div <- z.test(battery, sigma.x = sigma, conf.level = 0.95)$conf.int
cat(sprintf('置信区间是: [%s, %s]', round(interval_div[1], 4),round(interval_div[2], 4),))
p_value <- pnorm(x, mean = a, sd = s/sqrt(n))
#t分布的置信区间求法
interval_div<-t.test(battery, mu = 20, alternative = "less", conf.level = 0.95)$conf.int
cat(sprintf('置信区间是: [%s, %s]', round(interval_div[1], 4),round(interval_div[2], 4),))
p_value <- pt(x,df,ncp)

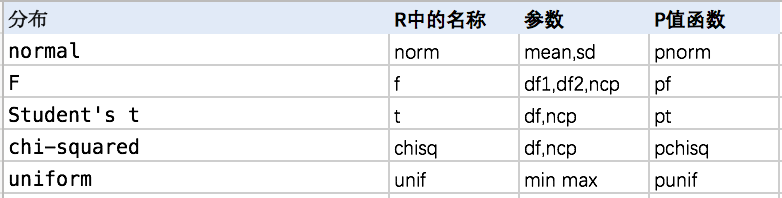
参数估计与假设检验之间的相同点、联系与区别：
相同点：都是根据样本信息对总体的数量特征进行推断；以样本分布为理论依据，建立在概率论基础之上的统计推断，推断结果都有一定的可信程度或风险。
联系：二者可相互转换，形成对偶性。对同一问题的参数进行推断，由于二者使用同一样本、同一统计量、同一分布，因而二者可以相互转换。区间估计问题可以转换成假设问题，假设问题也可以转换成区间估计问题。区间估计中的置信区间对应于假设检验中的接受区域，置信区间以外的区域就是假设检验中的拒绝域。
主要区别：参数估计是以样本资料估计总体参数的真值，假设检验是以样本资料检验对总体参数的先验假设是否成立；参数估计中的区间估计是求以样本统计量为中心的双侧置信区间，假设检验既有双侧检验，也有单侧检验；参数估计中的区间估计是以大概率为标准，通常以较大的把握程度（置信水平）1-α去保证总体参数的置信区间。而假设检验是以小概率原理为标准，通常是给定很小的显著性水平α去检验对总体参数的先验假设是否成立或对总体的分布的形式的假设进行判断。
参考：
第5章：参数估计与假设检验 | 统计分析（以R语言为工具）：辅助材料
科学网-在R中如何求给定分布和统计量的p-value - 彭友松的博文
参数估计、假设检验及它们之间的关系（相同点、联系与区别）_ccccplus的博客-CSDN博客_参数估计与假设检验的区别和联系

卡卡

这么说吧，直观一些，区间估计，是基于样本，做推断，做猜测。假设检验就是反过来，基于样本，做判断，做决策。
我不想给你讲太多理论的东西，具体可以看Eric Lehmann的两本书，点估计理论，TPE和检验统计假设，TSH。后面这个名字是我自己翻译的，哈哈。第三章，有很漂亮的解释，学的时候读了十几遍，很推荐。
说到具体的，还是用例子吧，举 肯定比讲什么概率一类的直观。既然说到栗子，就用栗子。比如一个大农场，种了很多栗子树，一年收了好几吨栗子，但是你想知道这些栗子大不大，平均重量是多少。那么你肯定知道，接下来要做的就是，随机地跳进筐里，抓两把栗子出来，一个一个称分量，然后记录。那么好啦，接下来我们就一一对应这些方法和概念。你跳进去的栗子海，这个叫整体，平均每个栗子的重量，这个叫做miu，整体的参数，也是我们要估计的参数。你两把抓出来的每个栗子叫样本，独立的，从同一个整体抽出来的，所以叫iid，独立同分布。这些样本的平均重量叫做X上面有个横线，X bar，我们要做的就是用样本估计整体。相信你对区间估计的公式很清楚，我就不用一个手机敲了。那么你看，假定你这两把抓的挺多，浩克的爪子，抓了49个栗子，这个就是样本量n，在分母上，分子是方差，就是样本的方差，最后再一起来个平方根，为啥是这样，你可以去推导下Var(Xbar)。前面再乘以一个正态分布的分位点，比如1.96，比如1.645，取决于你的alpha。这个区间算出来，就是说，我有1－alpha的信心，我抽样的这个区间，能够覆盖住miu，也就是准确地抓住。这个说法是合理的，因为n越大，区间越小，的确，你抽样越多，当然越有把握。如果你是松鼠爪子，只抓了几个，这个就要用t分布。顺便提一句，t分布所有的值都大于正态分布，因为它扁，尾巴粗，肚子小。
那么接下来说假设检验，这个就要用更多的情形。比如种栗子前，你听人家说，你这个品种都是大栗子，平均每个都是25克，结果你种完了收获的时候，看着一个个小巧的不行。所以你要抽样看看他们到底说对没有。因此呢，你进行了完全同样的操作，结果，比如说，你抽出来的49个栗子，平均只有23克，标准差0.7克。那好，现在原假设，就是miu=25，备择假设可以是miu≠25或者miu<25。这样一来，你就要算统计量了。我还是不写公式，因为你会算，出来就是20，你一查表，天，20倍标准差，你就可以说，我认为，你们是在骗我，根本就没有那么大的栗子。拒绝原假设。
从上面两段，你应该可以看出，假设检验最终是一个结论，就是定性的结论，当然里面还有一个终极问题就是，假设检验无法证实，无法接受原假设，这个问题就另外讨论了。而区间估计，也经常叫置信区间，英文的confidence，就是在做一定的估计，有信心说我做的这个区间能覆盖住。当然这些都是频数统计学下的说法，更多的就先不说了。希望能有帮助。

大力水手

结论：区间估计和假设检验有极大的相似性，因为他们都是基于枢轴量(Pivot)的统计推断。两者的区别在于解决的问题不相同。
先举个例子，假设样本服从正态分布  ，而方差 已知。考虑关于均值的假设检验问题： 。则显著性水平为 下的拒绝域为 . 因此，接受域为 . 而置信水平为 的置信区间为 。
乍看之下，统计推断中的接受域似乎就是置信区间。而且在其他的例子中，这种规律依然存在。这并不是纯粹的巧合，我们称之为区间估计和假设检验的二重性(Duality)。存在这种相似性的原因是因为他们都是基于相同的出发点——枢轴量。

• 相似性：
  

我们先回忆一下两者的定义。（为简化起见，以下只对连续型变量考虑。）
区间估计是找到一个随机的区间，使得区间包含真实参数的概率等于一个固定的值 ，我们称这个值为置信水平。假设检验是去判断某个假设是否真实，使得在原假设真实的情况下，犯错的概率等于一个固定的值 ，我们称之为显著性水平。
由于被估计或被推断的参数是未知的，如上面例子中的均值 ，因此我们必须找到一个变量，使得他的分布已知。我们称这种变量叫做枢轴量。举例而言，对于上面的例子，我们可以选取变量 为枢轴量，而其分布已知为标准正态分布。
在枢轴量的基础下，如果我们想进行区间估计，即找到一个区间使得区间包含真实参数的概率等于 ，我们可以限制 ;如果我们想进行统计推断，即在原假设真实的情况下，犯错的概率等于 ，我们可以限制 .因此，两者求解出来的应该是等价的。
更一般的而言，对于任意的区间估计及假设检验问题，置信水平为 的区间估计和显著性水平为 的统计推断等价。而这种等价正是基于两者有相同的出发点——枢轴量。

• 区别：
  

两者的最大区别在于解决问题的不相同。相比于区间估计，统计推断对参数有一定的假设，即除非在数据及其不可能在原假设中发生时时，倾向于不拒绝原假设。这个性质使得统计推断对于参数有倾向性。然而区间估计并没有作出任何假设，它只是计算了一个随机区间。在数据量极少或样本的方差巨大的时候，或许假设推断会声称自己的原假设正确，如 ，但区间估计则会给出一个很大的范围，如 。

• 再出一个我常常问的面试题吧：
  

假设有两个机器随机独立的生成1或0，即Bernoulli分布 。机器A以10%的概率生成1，而机器B以20%的概率生成1。请设计一个实验，要求分辨数据是从机器A生成的还是机器B生成的（检测方法，样本数量，如何改进）。
Hint：做假设检验的小伙伴都被拒了噢( >﹏<。)～

长长的路

学了一半的统计学，感觉这门学科一个重要作用就是研究通过抽取样本来对总体进行研究。
置信水平，根据一次抽样，来估计总体的情况，以及可靠性：
比如你出了一道题，让10000名学生作答，答完题后，想知道多少人答对了，无奈总体太大，一下子看不过来，怎么办，那就抽取100份试卷，看看答对的比例有多少。 如果70名学生答对了，那就能计算期望（平均值）和方差（偏差度）。 再根据中心极限定理得知，抽样平均值会形成一个正态分布（假设不断抽取100份试卷，计算每次抽样的平均值，抽上100次，每次的平均值就形成了正态分布），根据标准正态分布属性（2个标准差内概率是95%），就可以得出结论：有95%的把握，这10000份答卷中，答对的估计有7000份，误差范围是2个标准差，这就是置信水平，根据一次抽样，来估计总体的情况。
而假设检验，就是已经知道总体情况，随着A条件发生变化，再进行一次抽样，来检验A条件的影响。或者已经有一个总体情况的结论，但不知道是否可靠，然后通过抽样进行检验。其计算理论基础和置信水平一样，默认抽样均值分布是正态分布。
如你看完了10000份卷子，正好得出有70%的同学是答对的。此时如果你想知道噪音对答题的影响，那么就让同一批学生在噪音环境中答题（两次答题互不影响）。那是否有影响呢？如果你不想再批这10000份卷子，你还是抽取100份卷子，发现有65份是答对的，结论怎么下？ 这就需要用到假设检验，假设没影响，那么出现随机抽100份，65份是对的概率多大，一般会约定，如果这个概率小于5%，那就假设出错，得出噪音对答题有影响的结论。

同花顺

二者都属于推断统计——利用样本的数据得到样本统计量，然后做出对总体参数的论断。
不同之处在于：用统计量推断参数时，如果参数未知，则这种推断叫参数估计——用统计量估计未知的参数；如果参数已知（或假设已知），需要利用统计量检验已知的参数是否靠谱，此时的统计推断即为假设检验。
举例来说：推断全校学生的平均每天上网时间。因为参数未知，要靠抽样的数据进行推断，此时进行的就是参数估计，用抽样得到的统计量——样本平均上网时间（比如说3小时）来估计全校学生平均上网时间。
如果先前有人已得出得出论断，学生平均上网时间为5小时，而你不知该参数可不可信，这时做的就是假设检验，通过样本得到的平均3小时的上网时间告诉你，先前关于总体的平均上网时间为5小时这一信息很可能是不靠谱的，无法通过检验。
========================
关于置信水平与显著水平的联系，你的等式正确。置信度越高，显著水平的值越低（但统计上却说越显著）。