金桔
金币
威望
贡献
回帖0
精华
在线时间 小时
|
登陆有奖并可浏览互动!
您需要 登录 才可以下载或查看,没有账号?立即注册


×
我们为什么要假设检验
我们在生活中经常会遇到对一个总体数据进行评估的问题,但我们又不能直接统计全部数据,这时就需要从总体中抽出一部分样本,用样本来估计总体情况。
举一个简单的例子:
学而思网校App进行了改版迭代,现在有以下两个版本
版本1:首页为一屏课程列表 ; 版本2:首页为信息流
如果我们想区分两个版本,哪个版本用户更喜欢,转化率会更高。我们就需要对总体(全部用户)进行评估,但是 并不是全部存量用户都会访问App,并且每天还会新增很多用户,所以我们无法对总体(全部用户)进行评估,我们只能从总体的用户中随机抽取样本(访问App)的用户进行分析,用样本数据表现情况来充当总体数据表现情况,以此来评估哪个版本转化率更高。
假设检验定义
假设检验是先对总体参数提出一个假设值,然后利用样本信息判断这一假设是否成立
假设检验的假设
由定义可知,我们需要对结果进行假设,然后拿样本数据去验证这个假设。
所以做假设检验时会设置两个假设:
一种叫原假设,也叫零假设,用H0表示。原假设一般是统计者想要拒绝的假设。原假设的设置一般为:等于=、大于等于>=、小于等于<=。
另外一种叫备择假设,用H1表示。备则假设是统计者想要接受的假设。备择假设的设置一般为:不等于、大于>、小于<。
例子在进行假设检验时,我们希望接受版本2的假设,想拒绝接受版本1的假设。所以我们的假设设置为:H0 :μ版本1 >= μ版本2 ,H1 : μ版本1 < μ版本2。
为什么统计者想要拒绝的假设放在原假设呢?因为原假设备被拒绝如果出错的话,只能犯第I类错误,而犯第I类错误的概率已经被规定的显著性水平所控制。有点看不懂哈?没关系我们讲一下假设检验中的两种错误和显著性水平就清楚了。
弃真错误、取伪错误
我们通过样本数据来判断总体参数的假设是否成立,但样本时随机的,因而有可能出现小概率的错误。这种错误分两种,一种是弃真错误,另一种是取伪错误。
弃真错误也叫第I类错误或α错误:它是指 原假设实际上是真的,但通过样本估计总体后,拒绝了原假设。明显这是错误的,我们拒绝了真实的原假设,所以叫弃真错误,这个错误的概率我们记为α。这个值也是显著性水平,在假设检验之前我们会规定这个概率的大小。
取伪错误也叫第II类错误或β错误:它是指 原假设实际上假的,但通过样本估计总体后,接受了原假设。明显者是错误的,我们接受的原假设实际上是假的,所以叫取伪错误,这个错误的概率我们记为β。
现在清楚原假设一般都是想要拒绝的假设了么?因为原假设备被拒绝,如果出错的话,只能犯弃真错误,而犯弃真错误的概率已经被规定的显著性水平所控制了。这样对统计者来说更容易控制,将错误影响降到最小。
显著性水平
显著性水平是指当原假设实际上正确时,检验统计量落在拒绝域的概率,简单理解就是犯弃真错误的概率。这个值是我们做假设检验之前统计者根据业务情况定好的。
显著性水平α越小,犯第I类错误的概率自然越小,一般取值:0.01、0.05、0.1等
当给定了检验的显著水平a=0.05时,进行双侧检验的Z值为1.96,t值为 。
当给定了检验的显著水平a=0.01时,进行双侧检验的Z值为2.58 。
当给定了检验的显著水平a=0.05时,进行单侧检验的Z值为1.645 。
当给定了检验的显著水平a=0.01时,进行单侧检验的Z值为2.33
检验方式
检验方式分为两种:双侧检验和单侧检验。单侧检验又分为两种:左侧检验和右侧检验。
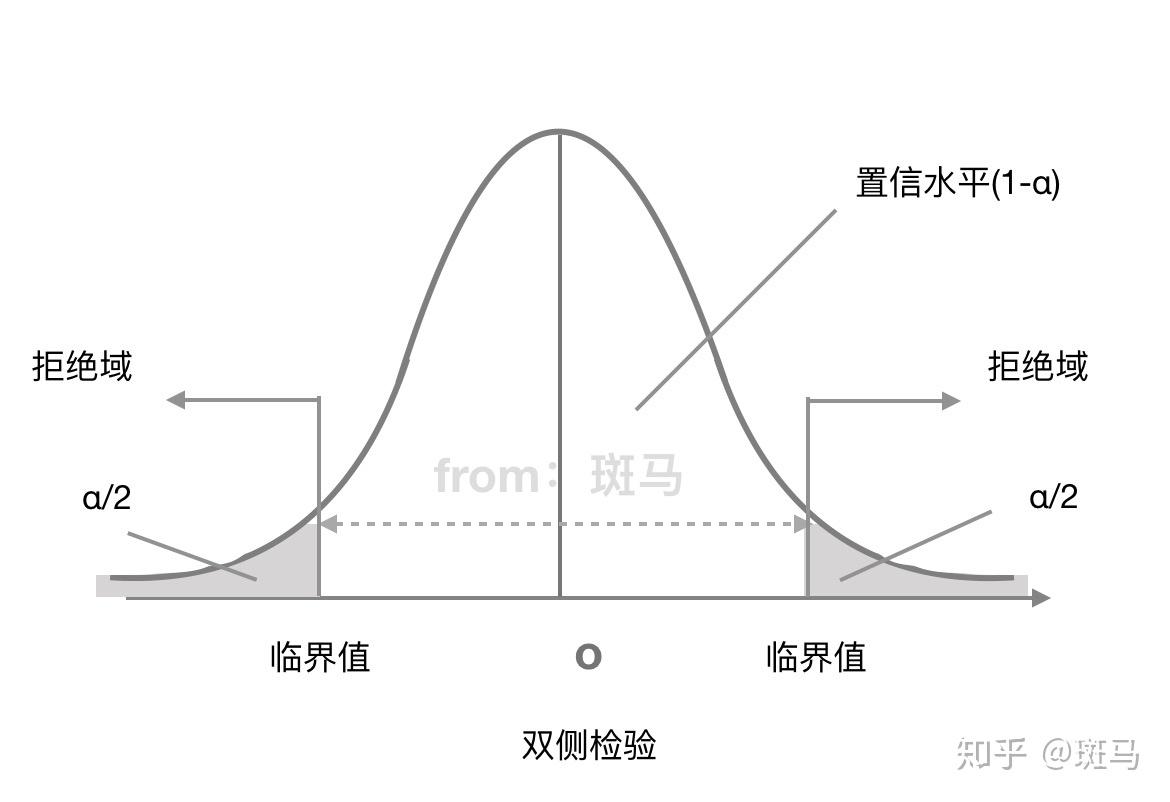
双侧检验:备择假设没有特定的方向性,形式为“≠”这种检验假设称为双侧检验
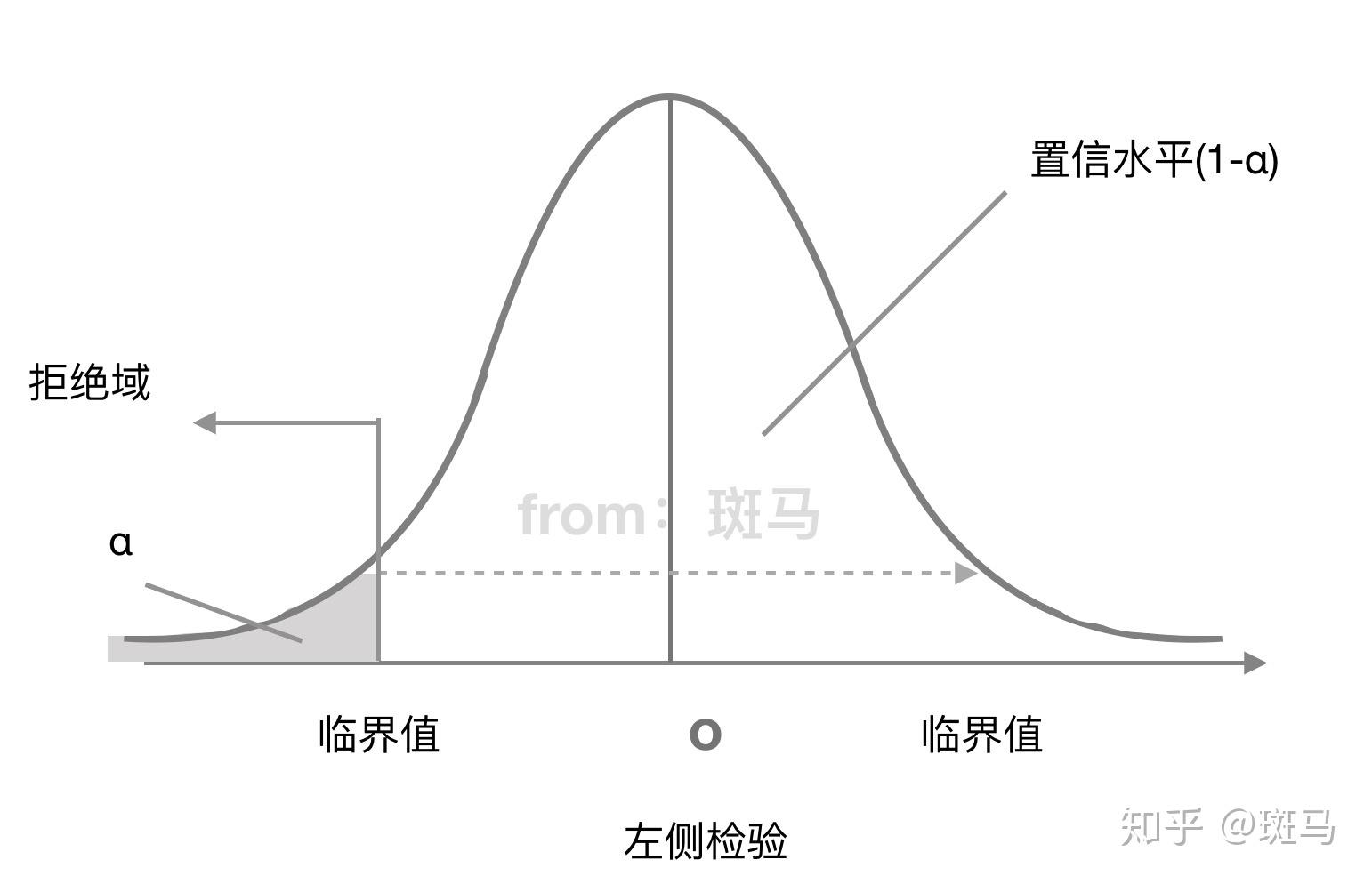
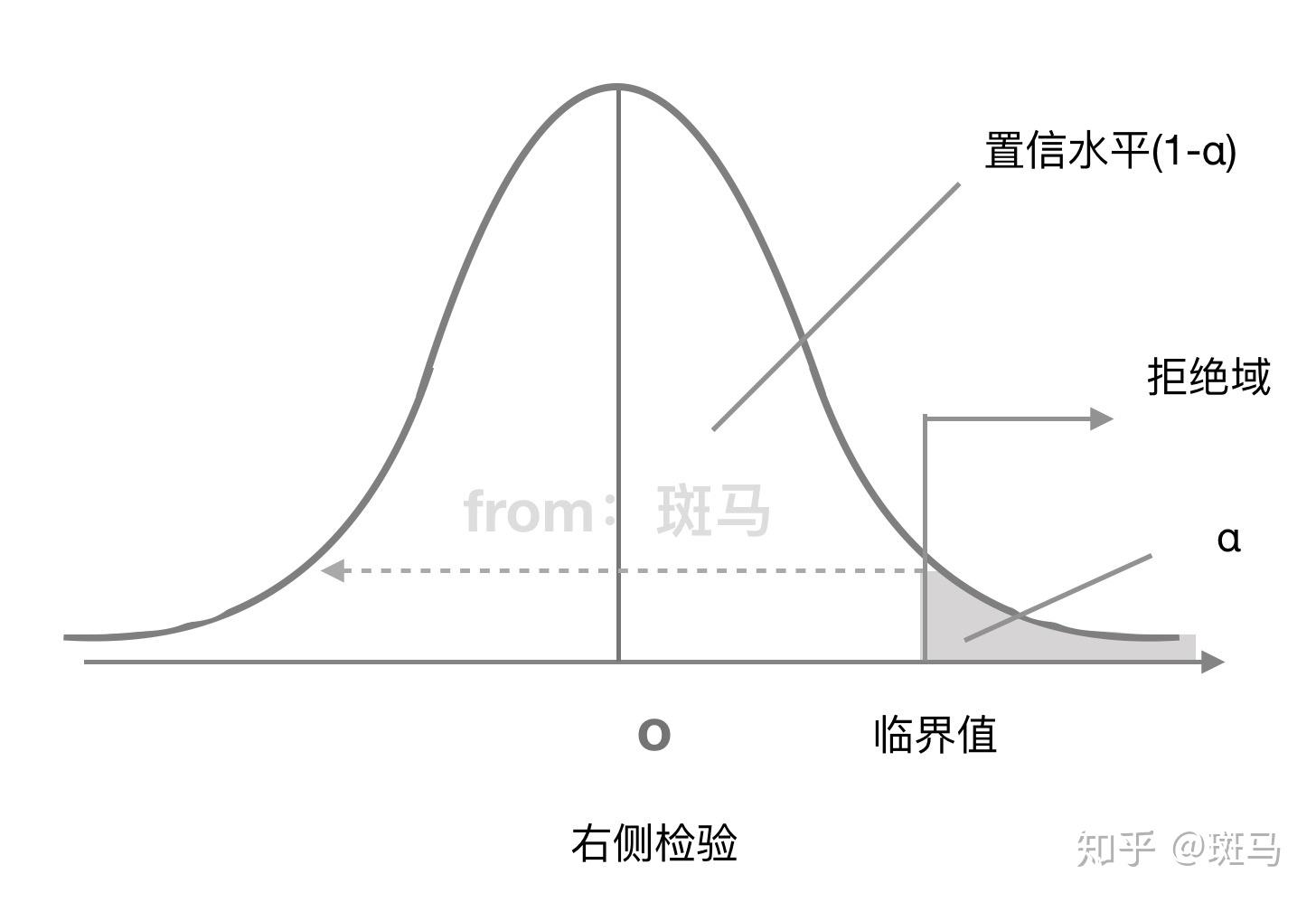
单侧检验:备择假设带有特定的方向性 形式为">""<"的假设检验,称为单侧检验 "<"称为左侧检验 ">"称为右侧检验
检验统计量
定义:据以对原假设和备择假设作出决策的某个样本统计量,称为检验统计量。
拒绝域
定义:拒绝域是由显著性水平围成的区域
拒绝域的功能主要用来判断假设检验是否拒绝原假设的。如果样本观测计算出来的检验统计量的具体数值落在拒绝域内,就拒绝原假设,否则不拒绝原假设。给定显著性水平α后,查表就可以得到具体临界值,将检验统计量与临界值进行比较,判断是否拒绝原假设。
双侧检验拒绝域:
左侧检验拒绝域:
右侧检验拒绝域:
假设检验步骤
- 提出原假设与备择假设
- 从所研究总体中出抽取一个随机样本
- 构造检验统计量
- 根据显著性水平确定拒绝域临界值
- 计算检验统计量与临界值进行比较
两种假设检验
假设检验根据业务数据分为两种:一个总体参数的假设检验和两个总体参数的假设检验
一个总体参数的假设检验:只有一个总体的假设检验
举个例子:学而思App原版本1转化率为 19%,学而思App版本2开发完成后,直接全量发布整体上线,过一段时间后统计转化率为27%,我们想判断版本2是否比版本1好,这时我们做的假设检验总体只有1个,全部用户。对于总体只有一个的称为一个总体参数的假设检验。
两个总体参数的假设检验:有两个总体的假设检验
同样的例子:学而思App版本1和学而思App版本2同时上线,流量各50%,这时我们做的假设检验总体有2个,分别为命中版本1的全部用户与命中版本2的全部用户。
两种假设检验的检验统计量计算方式有所不同,所以做区分描述。
一个总体参数的假设检验:
大小样本:样本量大于等于30的样本称为大样本,样本量小于30的样本称为小样本。
一个总体参数的大样本(n \geq30 )假设检验方法:
假设形式:
双侧检验:H0 : \mu=\mu0 , H1 : \mu\ne\mu0 ;
左侧检验:H0: \mu\geq\mu0 , H1 : \mu\ < \mu0 ;
右侧检验:H0: \mu\leq\mu0 , H1 : \mu > \mu0 ;
检验统计量:
\sigma已知 :z=\frac{\bar{x}-\mu0}{\sigma/\sqrt{n}} \sigma未知 :z = \frac{\bar{x}-\mu0}{s/\sqrt{n}}
\bar{x}:样本均值
\mu:假设的总体均值
s:样本标准差
\sigma:总体标准差 :当总体标准差已知时,用 \sigma 参与计算更精准。
n:样本量
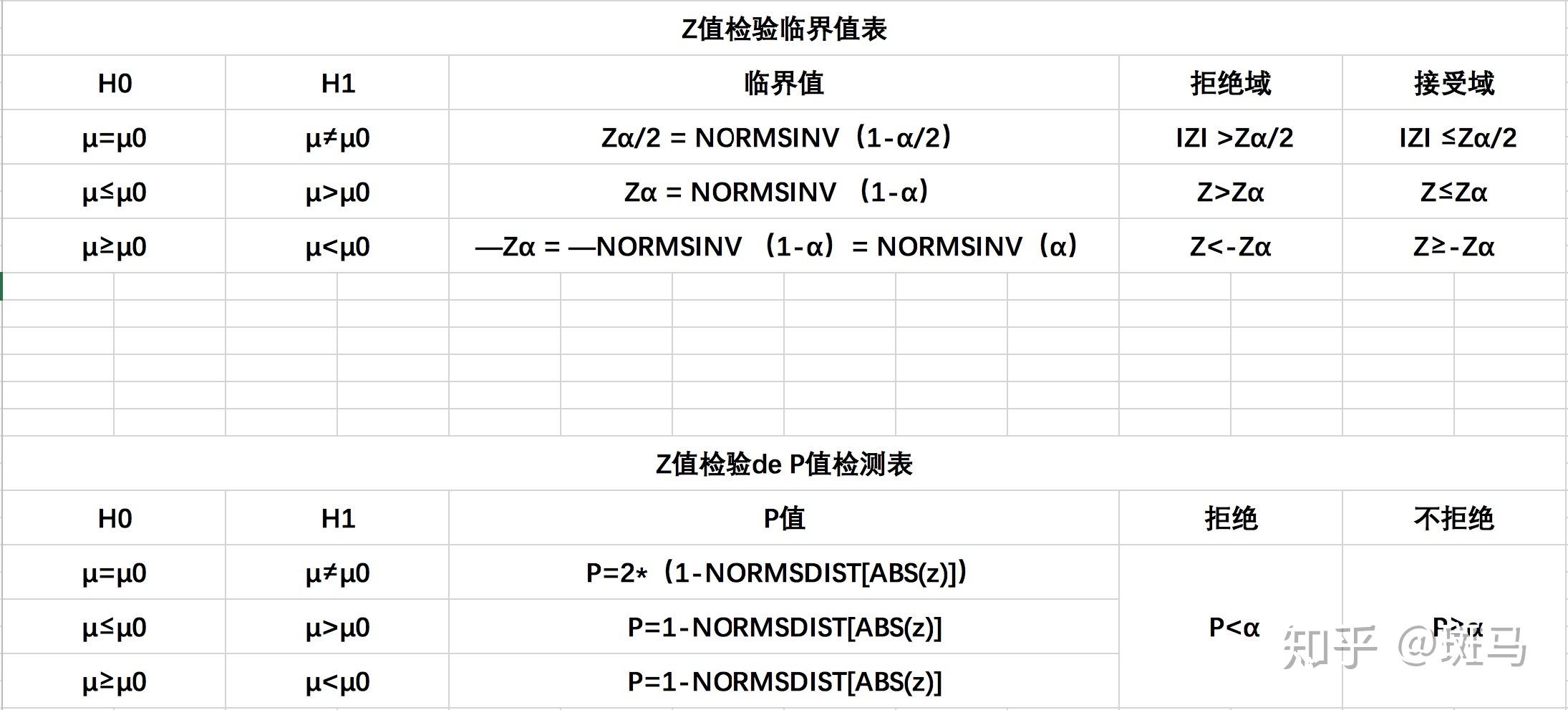
\alpha与拒绝域 :
双侧检验:\left| Z \right| > Z\alpha/2
左侧检验: Z < -Z\alpha
右侧检验: Z > Z\alpha
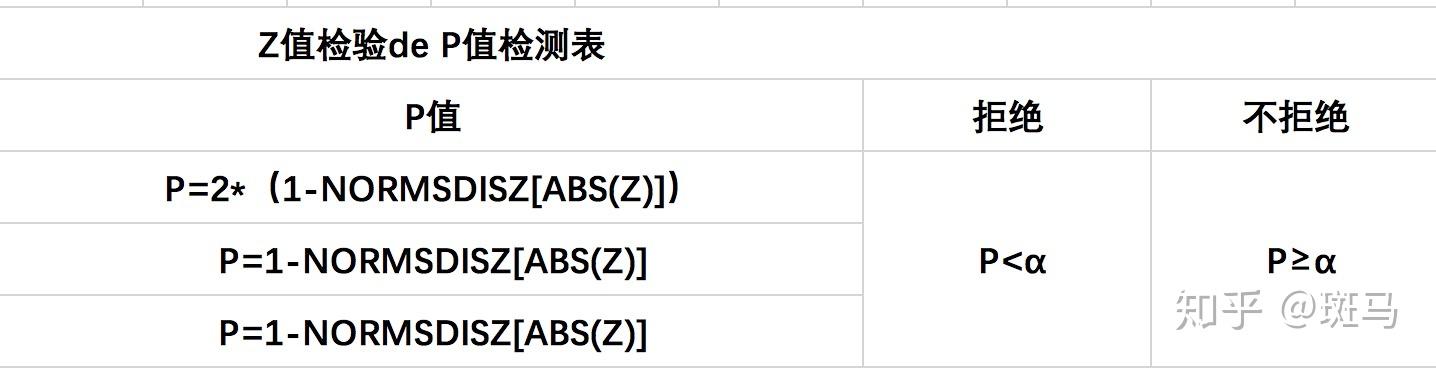
P值决策:
P< \alpha ,拒绝H0

一个总体参数的小样本(n<30)假设检验方法:
假设形式:
双侧检验:H0 : \mu=\mu0 , H1 : \mu\ne\mu0 ;
左侧检验:H0: \mu\geq\mu0 , H1 : \mu\ < \mu0 ;
右侧检验:H0: \mu\leq\mu0 , H1 : \mu > \mu0 ;
检验统计量:
\sigma已知 :t=\frac{\bar{x}-\mu0}{\sigma/\sqrt{n}} \sigma未知 :t = \frac{\bar{x}-\mu0}{s/\sqrt{n}}
\bar{x}:样本均值
\mu:假设的总体均值
s:样本标准差
\sigma:总体标准差 :当总体标准差已知时,用 \sigma 参与计算更精准。
n:样本量
\alpha与拒绝域 :
双侧检验:\left| t \right| > t\alpha/2(n-1)
左侧检验: t < -t\alpha(n-1)
右侧检验: t > t\alpha(n-1)
t值怎么看:
n 是样本量=10、自由度=n-1。当α=0.05时,临界值-双侧检验:t0.025(9) 单侧检验t0.05(9)
P值决策:
P< \alpha ,拒绝H0


一个总体成数的假设检验:
定义:
样本成数:它是指样本中具有某一相同标志表现的单位数占样本容量的比重,记为p.
总体成数:它是指总体中具有某一相同标志表现的单位数占全部总体单位数的比重,一般用π表示.
假设形式:
双侧检验: H0 : \pi = \pi0 , H1 : \pi\ne\pi0
左侧检验: H0 : \pi\geq\pi0 , H1 : \pi<\pi0
右侧检验: H0 : \pi \leq\pi0 , H1 : \pi >\pi0
检验统计量:
z=\frac{P-\pi0}{\sqrt{\frac{\pi0(1-\pi0)}{n}}}
P: 样本成数
\pi0: 总体成数
n:样本量
\alpha 与拒绝域:
双侧检验:\left| Z \right| > Z\alpha/2
左侧检验: Z < -Z\alpha
右侧检验: Z > Z\alpha
P值决策:
P< \alpha ,拒绝H0

两个总体参数的假设检验
大小样本:样本量大于等于30的样本称为大样本,样本量小于30的样本称为小样本。
两个总体参数的大样本(n \geq30 )假设检验方法:
假设形式:
双侧检验: H0 : \mu1-\mu2 = 0 , H1 :\mu1 - \mu2 \ne 0 ;
左侧检验: H0 : \mu1 - \mu2 \ \geq 0 , H1 : \mu1 - \mu2 < 0 ;
右侧检验: H0 : \mu1 - \mu2 \leq 0 ,H1 : \mu1 - \mu2 >0 ;
检验统计量
t=\frac{(\bar{x1} - \bar{x2})-(\mu1-\mu2)}{\sqrt{s1^{2}/n1+s2^{2}/n2}}
\mu:两个总体均值
\bar{x}: 两个样本均值
s:样本标准差
\sigma:总体标准差 :当总体标准差已知时,用 \sigma 参与计算更精准。
n:两个样本量
\alpha与拒绝域 :
双侧检验:\left| Z \right| > Z\alpha/2
左侧检验: Z < -Z\alpha
右侧检验: Z > Z\alpha
P值决策:
P< \alpha ,拒绝H0

两个总体成数的假设检验
当n1*P1、n1*(1-P1)、n2*P2、n2*(1-p2)都大于或等于5时,就可以称为大样本。
假设形式:
双侧检验:H0 : π1-π2 =0 ,H1 : π1-π2≠0
左侧检验:H0 : π1-π2 ≥0 ,H1 : π1-π2<0
右侧检验:H0 : π1-π2 ≤0 ,H1 : π1-π2>0
检验统计量:
(1)原假设为 H0 : \pi1 = \pi2 或 π1-π2 ≥0 、π1-π2 ≤0情况下。
检验统计量:
z=\frac{p1-p2}{\sqrt{p(1-p)(1/n1+1/n2)}}
p1、p2:两个样本成数
p:两个样本的合并成数 p=\frac{p1*n1+p2*n2}{n1+n2}
n1、n2:两个样本量
(2)原假设为 H0 : \pi1-\pi2 = d0(d0\ne0)
检验统计量:
z= \frac{(p1-p2)-d0}{\sqrt{p1(1-p1)/n1+p2(1-p2)/n2}}
\alpha与拒绝域 :
双侧检验:\left| Z \right| > Z\alpha/2
左侧检验: Z < -Z\alpha
右侧检验: Z > Z\alpha
P值决策:
P< \alpha ,拒绝H0
R语言实现假设检验
z.test():BSDA包,调用格式
z.test(x, y = NULL, alternative = "two.sided,less,right", mu = 0, sigma.x = NULL, sigma.y = NULL, conf.level = 0.95)x,y为样本数据,单样本时忽略y;alternative选择检验类型,two.sided 双侧检验,less左侧检验,greater右侧检验 ;mu为原假设的均值;sigma.x,sigma.y为标准差;conf.level为置信水平,var.equal是逻辑变量,var.equal=TRUE表示两样品方差相同,var.equal=FALSE(缺省)表示两样本方差不同
t.test():调用格式
t.test(x, y = NULL, alternative=c("two sided","less","greater"), mu = 0,paired = TRUE, var.equal = FALSE, conf.level = 0.95,...)x,y为样本数据,单样本时忽略y;alternative选择检验类型,two.sided 双侧检验,less左侧检验,greater右侧检验 ;mu为原假设的均值;sigma.x,sigma.y为标准差;conf.level为置信水平,var.equal是逻辑变量,var.equal=TRUE表示两样品方差相同,var.equal=FALSE(缺省)表示两样本方差不同
binom.test():调用格式
binom.test(x, n, p = 0.5,alternative = c("two.sided", "less", "greater"),conf.level = 0.95)其中x是成功的次数;n是试验总数,P是原假设的概率。也是总体成数的公式
原文地址:https://zhuanlan.zhihu.com/p/86178674 |
|
 /3
/3 